–£—á–Ķ–Ĺ–ł—ā–Ķ –ł —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą–ł—ā–Ķ –ĺ—ā–ļ—Ä–į–Ļ –≤—Ä–Ķ–ľ–Ķ –ĺ–Ī–ł—á–į—ā –ī–į –∑–į–Ņ—ä–Ľ–≤–į—ā –≤—Ä–Ķ–ľ–Ķ—ā–ĺ –ł —Ā–ļ—É–ļ–į—ā–į —Ā–ł, –ļ–į—ā–ĺ –∑–į–ī–į–≤–į—ā –Ņ–ĺ–ľ–Ķ–∂–ī—É —Ā–ł –Ĺ–Ķ—Ä–į–∑—Ä–Ķ—ą–ł–ľ–ł –∑–į–ī–į—á–ł –ł –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–ł. –í–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ –∑–Ľ–ĺ—Ä–į–ī—Ā—ā–≤–į—ā, –ļ–ĺ–≥–į—ā–ĺ –≥–Ľ–Ķ–ī–į—ā –ļ–į–ļ –Ĺ—Ź–ļ–ĺ–Ļ –Ņ–ĺ-–≥–Ľ—É–Ņ–į–≤ –ĺ—ā —ā—Ź—Ö —Ā–Ķ –ľ—ä—á–ł –ł –Ņ–ĺ—ā–ł –ī–į —Ä–į–∑—Ä–Ķ—ą–ł –Ĺ–Ķ—Ä–į–∑—Ä–Ķ—ą–ł–ľ–ĺ—ā–ĺ. –ź–∑ —Ā–ł —Ā–Ņ–ĺ–ľ–Ĺ—Ź–ľ, —á–Ķ –Ņ—Ä–Ķ–ī–ł –≥–ĺ–ī–ł–Ĺ–ł —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į—Ö–į –ł –ļ–Ĺ–ł–∂–ļ–ł —Ā –≥–Ľ–į–≤–ĺ–Ī–Ľ—ä—Ā–ļ–į–Ĺ–ł—Ü–ł, –Ĺ–ĺ –Ĺ–Ķ –∑–Ĺ–į–ľ –∑–į—Č–ĺ –≤–Ķ—á–Ķ —ā–Ķ –Ĺ–Ķ —Ā–Ķ —Ā—Ä–Ķ—Č–į—ā —á–Ķ—Ā—ā–ĺ. –ú–ĺ–∂–Ķ –Ī–ł –Ĺ—Ź–ľ–į –ļ–ĺ–Ļ –ī–į –≥–ł —á–Ķ—ā–Ķ?
–ď–ĺ–Ľ—Ź–ľ –Ī—Ä–ĺ–Ļ –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–ł –ł –≥–Ľ–į–≤–ĺ–Ī–Ľ—ä—Ā–ļ–į–Ĺ–ł—Ü–ł —Ā—ä—Ö—Ä–į–Ĺ—Ź–≤–į—ā —Ā–≤–ĺ—Ź—ā–į –į–ļ—ā—É–į–Ľ–Ĺ–ĺ—Ā—ā –ĺ—ā –ľ–Ĺ–ĺ–≥–ĺ –≥–ĺ–ī–ł–Ĺ–ł –ł —Ā–į –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ –∑–į –Ĺ–Ķ—Ā—ä–≤—ä—Ä—ą–Ķ–Ĺ—Ā—ā–≤–ĺ—ā–ĺ –Ĺ–į –ľ–Ĺ–ĺ–≥–ĺ –ĺ—ā –Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ–ł—ā–Ķ –Ĺ–į—É—á–Ĺ–ł —ā–Ķ–ĺ—Ä–ł–ł, –Ĺ—Ź–ļ–ĺ–ł –ĺ—ā –ļ–ĺ–ł—ā–ĺ –ī–ĺ—Ä–ł —Ā–į —Ā—á–ł—ā–į–Ĺ–ł –∑–į —Ą—É–Ĺ–ī–į–ľ–Ķ–Ĺ—ā–į–Ľ–Ĺ–ł. –ē—ā–ĺ –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –ĺ—ā –Ĺ–į–Ļ-–Ņ–ĺ–Ņ—É–Ľ—Ź—Ä–Ĺ–ł—ā–Ķ –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–ł, –į –į–ļ–ĺ —ā–Ķ —Ā–į –≤–ł –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ĺ–ł, —Ā —Ä–į–ī–ĺ—Ā—ā –Ī–ł—Ö –≤–ł –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–ł–Ľ –ĺ—Č–Ķ –ľ–Ĺ–ĺ–≥–ĺ.
–ź—Ö–ł–Ľ –ł –ļ–ĺ—Ā—ā–Ķ–Ĺ—É—Ä–ļ–į—ā–į
–ü–į—Ä–į–ī–ĺ–ļ—Ā—ä—ā –∑–į –ī—Ä–Ķ–≤–Ĺ–ĺ–≥—Ä—ä—Ü–ļ–ł—Ź –≥–Ķ—Ä–ĺ–Ļ –ź—Ö–ł–Ľ –ł –ļ–ĺ—Ā—ā–Ķ–Ĺ—É—Ä–ļ–į—ā–į –Ķ –Ķ–ī–Ĺ–į –į–Ņ–ĺ—Ä–ł—Ź (–Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ł –≤—Ź—Ä–Ĺ–ĺ, –Ĺ–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł–≤–ĺ –ł–∑–ļ–į–∑–≤–į–Ĺ–Ķ), —Ā—ä—Ā—ā–į–≤–Ķ–Ĺ–į –ĺ—ā –ī—Ä–Ķ–≤–Ĺ–ĺ–≥—Ä—ä—Ü–ļ–ł—Ź —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą –ó–Ķ–Ĺ–ĺ–Ĺ –ĺ—ā –ē–Ľ–Ķ—Ź –ĺ—Č–Ķ –Ņ—Ä–Ķ–∑ V –≤–Ķ–ļ –Ņ—Ä–Ķ–ī–ł –Ĺ–ĺ–≤–į—ā–į –Ķ—Ä–į.
–ź—Ö–ł–Ľ —Ä–Ķ—ą–į–≤–į –ī–į —Ā–Ķ —Ā—ä—Ā—ā–Ķ–∑–į–≤–į –≤ –ī–ł—Ā—Ü–ł–Ņ–Ľ–ł–Ĺ–į—ā–į –Ī—Ź–≥–į–Ĺ–Ķ —Ā –Ķ–ī–Ĺ–į… –ļ–ĺ—Ā—ā–Ķ–Ĺ—É—Ä–ļ–į. –Ę—ä–Ļ –ļ–į—ā–ĺ –ļ–ĺ—Ā—ā–Ķ–Ĺ—É—Ä–ļ–ł—ā–Ķ –Ĺ–Ķ —Ā–į –ĺ—Ā–ĺ–Ī–Ķ–Ĺ–ĺ –Ī—ä—Ä–∑–ł –Ī–Ķ–≥–į—á–ł, –Ī–Ľ–į–≥–ĺ—Ä–ĺ–ī–Ĺ–ł—Ź—ā –≥–Ķ—Ä–ĺ–Ļ –ł –ī–į–≤–į –Ņ—Ä–Ķ–ī–Ĺ–ł–Ĺ–į –ĺ—ā 500 –ľ–Ķ—ā—Ä–į. –Ę–ĺ–Ļ —Ź –ł–∑—á–į–ļ–≤–į –ī–į –ł–∑–ľ–ł–Ĺ–Ķ —ā–ĺ–≤–į —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –ł —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į –∑–į–Ņ–ĺ—á–≤–į –Ĺ–į–ī–Ņ—Ä–Ķ–≤–į—Ä–į—ā–į —ā–ł—á–į–Ļ–ļ–ł —Ā 10 –Ņ—ä—ā–ł –Ņ–ĺ-–≤–ł—Ā–ĺ–ļ–į —Ā–ļ–ĺ—Ä–ĺ—Ā—ā. –í —ā–ĺ–∑–ł —Ā–Ľ—É—á–į–Ļ, –ī–ĺ–ļ–į—ā–ĺ –ź—Ö–ł–Ľ –Ņ—Ä–ĺ–Ī—Ź–≥–į 500-—ā–Ķ –ľ–Ķ—ā—Ä–į, –ļ–ĺ—Ā—ā–Ķ–Ĺ—É—Ä–ļ–į—ā–į –Ķ –ł–∑–ľ–ł–Ĺ–į–Ľ–į –ĺ—Č–Ķ 50. –°–Ľ–Ķ–ī —ā–ĺ–≤–į –Ī–Ķ–≥–į—á—ä—ā –Ņ—Ä–Ķ–ĺ–ī–ĺ–Ľ—Ź–≤–į –ĺ—Č–Ķ 50 –ľ–Ķ—ā—Ä–į, –Ĺ–ĺ –≤–Ľ–Ķ—á—É–≥–ĺ—ā–ĺ –≤ —Ā—ä—Č–ĺ—ā–ĺ –≤—Ä–Ķ–ľ–Ķ –Ķ –ł–∑–ľ–ł–Ĺ–į–Ľ–ĺ –Ĺ–ĺ–≤–ł 5 –ľ–Ķ—ā—Ä–į. –í–Ķ—á–Ķ –≤–ł —Ā–Ķ —Ā—ā—Ä—É–≤–į —á–Ķ –≤—Ā–Ķ–ļ–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā —ā–ĺ–Ļ —Č–Ķ —Ź –ī–ĺ–≥–ĺ–Ĺ–ł –Ľ–ł?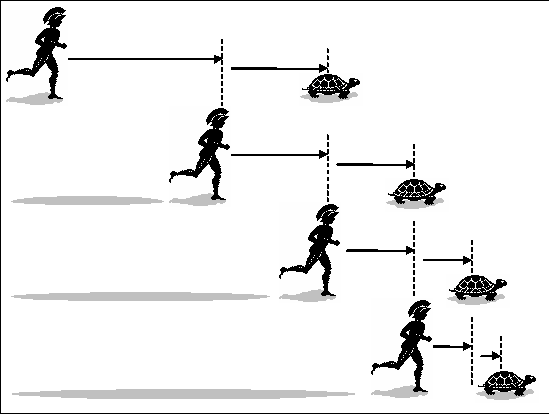
–ü—Ä–Ķ–∑ —Ā–Ľ–Ķ–ī–≤–į—Č–ł—Ź –≤—Ä–Ķ–ľ–Ķ–≤–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ –ź—Ö–ł–Ľ –Ņ—Ä–ĺ–Ī—Ź–≥–≤–į 5 –ľ–Ķ—ā—Ä–į, –į —ā—Ź —Ā–Ķ –Ķ –Ņ—Ä–ł–ī–≤–ł–∂–ł–Ľ–į –Ĺ–į 0,5 –ľ–Ķ—ā—Ä–į –ł —ā. –Ĺ. —Ä–į–∑—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ—ā–ĺ –ī–ĺ —ā—Ź—Ö —Ā–Ķ —Ā—ä–ļ—Ä–į—Č–į–≤–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ –ł —Ā–Ņ–ĺ—Ä–Ķ–ī –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į —ā–ĺ–Ļ –Ĺ–ł–ļ–ĺ–≥–į –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į —Ź –ī–ĺ—Ā—ā–ł–≥–Ĺ–Ķ.
–†–į–∑–Ī–ł—Ä–į —Ā–Ķ, –ĺ—ā –≥–Ľ–Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į –Ĺ–į —Ą–ł–∑–ł–ļ–į—ā–į —ā–ĺ–∑–ł –Ņ–į—Ä–į–ī–ĺ–ļ—Ā –Ķ –Ī–Ķ–∑—Ā–ľ–ł—Ā–Ľ–Ķ–Ĺ, –∑–į—Č–ĺ—ā–ĺ –Ī—ä—Ä–∑–ĺ —ā–ł—á–į—Č–ł—Ź—ā –ź—Ö–ł–Ľ —Ā–ļ–ĺ—Ä–ĺ —Č–Ķ —Ź –Ņ–ĺ–ī–ľ–ł–Ĺ–Ķ. –Ě–ĺ –ó–Ķ–Ĺ–ĺ–Ĺ –Ķ –ł—Ā–ļ–į–Ľ –ī–į –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–į —Ā —Ä–į–∑—Ā—ä–∂–ī–Ķ–Ĺ–ł—Ź—ā–į —Ā–ł, —á–Ķ –ł–ī–Ķ–į–Ľ–ł–∑–ł—Ä–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł—ā–Ķ –Ņ–ĺ–Ĺ—Ź—ā–ł—Ź „—ā–ĺ—á–ļ–į –≤ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–ĺ—ā–ĺ“ –ł „–ľ–ĺ–ľ–Ķ–Ĺ—ā –≤—ä–≤ –≤—Ä–Ķ–ľ–Ķ—ā–ĺ“ –Ĺ–Ķ–≤–ł–Ĺ–į–≥–ł —Ā–į –Ņ–ĺ–ī—Ö–ĺ–ī—Ź—Č–ł –∑–į –ļ–ĺ—Ä–Ķ–ļ—ā–Ĺ–ĺ—ā–ĺ –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –ļ—ä–ľ —Ä–Ķ–į–Ľ–Ĺ–ĺ—ā–ĺ –ī–≤–ł–∂–Ķ–Ĺ–ł–Ķ. –Ě–Ķ–≥–ĺ–≤–į—ā–į –į–Ņ–ĺ—Ä–ł—Ź –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–į —Ä–į–∑–Ľ–ł–ļ–į—ā–į –ľ–Ķ–∂–ī—É –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–į—ā–į –ĺ–Ī–ĺ—Ā–Ĺ–ĺ–≤–ļ–į –Ĺ–į —Ā–ł—ā—É–į—Ü–ł—Ź—ā–į –ł —Ä–Ķ–į–Ľ–Ĺ–ĺ—Ā—ā—ā–į. –ú–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ĺ—ā–ĺ —ā–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ –Ķ, —á–Ķ –Ĺ–Ķ–Ĺ—É–Ľ–Ķ–≤–ł—ā–Ķ –Ņ—Ä–ĺ—Ā—ā—Ä–į–Ĺ—Ā—ā–≤–Ķ–Ĺ–ĺ-–≤—Ä–Ķ–ľ–Ķ–≤–ł –ł–Ĺ—ā–Ķ—Ä–≤–į–Ľ–ł –ľ–ĺ–≥–į—ā –ī–į —Ā–Ķ –ī–Ķ–Ľ—Ź—ā –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ, –Ĺ–ĺ –į–ļ–ĺ —ā–ĺ–≤–į –Ī–Ķ—ą–Ķ —ā–į–ļ–į –ł –≤ —Ä–Ķ–į–Ľ–Ĺ–ĺ—Ā—ā—ā–į, —ā–ĺ –ź—Ö–ł–Ľ –∑–į–≤–ł–Ĺ–į–≥–ł —Č–Ķ—ą–Ķ –ī–į –ĺ—Ā—ā–į–≤–į –∑–į–ī –ļ–ĺ—Ā—ā–Ķ–Ĺ—É—Ä–ļ–į—ā–į.
–ü–į—Ä–į–ī–ĺ–ļ—Ā –Ĺ–į –≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ł—Ź –ļ–ĺ–Ĺ—ā—É—Ä
–ü–į—Ä–į–ī–ĺ–ļ—Ā–ł—ā–Ķ, –ĺ–Ņ–ł—Ā–≤–į—Č–ł –Ņ—ä—ā–Ķ—ą–Ķ—Ā—ā–≤–ł—Ź –≤—ä–≤ –≤—Ä–Ķ–ľ–Ķ—ā–ĺ, —Ā–į —Ā—ā—Ä–į—ą–Ĺ–ĺ –ľ–Ĺ–ĺ–≥–ĺ –Ĺ–į –Ī—Ä–ĺ–Ļ. –ė –ĺ—ā–ī–į–≤–Ĺ–į —Ā–į –Ľ—é–Ī–ł–ľ–ł –∑–į –Ņ–ł—Ā–į—ā–Ķ–Ľ–ł—ā–Ķ –Ĺ–į —Ą–į–Ĺ—ā–į—Ā—ā–ł–ļ–į, –ļ–į–ļ—ā–ĺ –ł –Ĺ–į —Ä–Ķ–∂–ł—Ā—Ć–ĺ—Ä–ł—ā–Ķ –ł —Ā—Ü–Ķ–Ĺ–į—Ä–ł—Ā—ā–ł—ā–Ķ –Ĺ–į —Ą–į–Ĺ—ā–į—Ā—ā–ł—á–Ĺ–ł —Ą–ł–Ľ–ľ–ł –ł —Ā–Ķ—Ä–ł–į–Ľ–ł. –°—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –≤–į—Ä–ł–į–Ĺ—ā–į –Ĺ–į –Ľ–ł–Ĺ–Ķ–Ļ–Ĺ–ł—ā–Ķ –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–ł –Ĺ–į –≤—Ä–Ķ–ľ–Ķ—ā–ĺ, –ļ–į—ā–ĺ –Ķ–ī–ł–Ĺ –ĺ—ā –Ĺ–į–Ļ-–Ņ—Ä–ĺ—Ā—ā–ł—ā–Ķ –Ķ –Ņ–ĺ—Ā–ĺ—á–Ķ–Ĺ –≤ –ļ–Ĺ–ł–≥–į—ā–į The New Time Travelers –ĺ—ā –Ē–Ķ–Ļ–≤–ł–ī –Ę—É–ľ–ł, –Ņ—Ä–ĺ—Ą–Ķ—Ā–ĺ—Ä –ĺ—ā —É–Ĺ–ł–≤–Ķ—Ä—Ā–ł—ā–Ķ—ā–į –≤ –ú–į—Ā–į—á—É–∑–Ķ—ā—Ā.

–ü—Ä–Ķ–ī—Ā—ā–į–≤–Ķ—ā–Ķ —Ā–ł, —á–Ķ –Ņ—ä—ā–Ķ—ą–Ķ—Ā—ā–≤–Ķ–Ĺ–ł–ļ—ä—ā –≤—ä–≤ –≤—Ä–Ķ–ľ–Ķ—ā–ĺ —Ā–ł –ļ—É–Ņ—É–≤–į –ĺ—ā –ļ–Ĺ–ł–∂–į—Ä–Ĺ–ł—Ü–į—ā–į —Ö–į—Ä—ā–ł–Ķ–Ĺ –Ķ–ļ–∑–Ķ–ľ–Ņ–Ľ—Ź—Ä –Ĺ–į —ā—Ä–į–≥–Ķ–ī–ł—Ź—ā–į „–•–į–ľ–Ľ–Ķ—ā“ –ĺ—ā –®–Ķ–ļ—Ā–Ņ–ł—Ä. –ź —Ā–Ľ–Ķ–ī —ā–ĺ–≤–į –ĺ—ā–ł–≤–į –Ĺ–į –Ņ—ä—ā–Ķ—ą–Ķ—Ā—ā–≤–ł–Ķ –Ĺ–į–∑–į–ī –ī–ĺ –≤—Ä–Ķ–ľ–Ķ—ā–ĺ –Ĺ–į –ļ—Ä–į–Ľ–ł—Ü–į—ā–į –ī–Ķ–≤–į (–ē–Ľ–ł–∑–į–Ī–Ķ—ā –Ņ—ä—Ä–≤–į). –Ę–į–ľ —Ā–Ķ —Ā—Ä–Ķ—Č–į —Ā –£–ł–Ľ—Ź–ľ –®–Ķ–ļ—Ā–Ņ–ł—Ä –ł –ľ—É –Ņ–ĺ–ī–į—Ä—Ź–≤–į –ļ–Ĺ–ł–≥–į—ā–į. –Ę–ĺ–Ļ –ĺ—ā —Ā–≤–ĺ—Ź —Ā—ā—Ä–į–Ĺ–į —Ö–≤–į—Č–į –ł —Ź –Ņ—Ä–Ķ–Ņ–ł—Ā–≤–į –ī–ĺ—Ā–Ľ–ĺ–≤–Ĺ–ĺ –ł —Ź –ł–∑–ī–į–≤–į –ļ–į—ā–ĺ —Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–ĺ —Ā—ä—á–ł–Ĺ–Ķ–Ĺ–ł–Ķ. –ú–ł–Ĺ–į–≤–į—ā –Ĺ–Ķ–ļ–ĺ–Ľ–ļ–ĺ—Ā—ā–ĺ—ā–ł–Ĺ –≥–ĺ–ī–ł–Ĺ–ł, –•–į–ľ–Ľ–Ķ—ā –Ķ –Ņ—Ä–Ķ–≤–Ķ–ī–Ķ–Ĺ –Ĺ–į —Ā—ā–ĺ—ā–ł—Ü–ł –Ķ–∑–ł—Ü–ł, –Ņ—Ä–Ķ–ł–∑–ī–į–≤–į–Ĺ –Ķ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ –ł –Ķ–ī–Ĺ–ĺ –ĺ—ā –ļ–ĺ–Ņ–ł—Ź—ā–į —Ā–Ķ –ĺ–ļ–į–∑–≤–į –≤ —Ā—ä—Č–ł—Ź—ā —ā–ĺ–∑–ł –ľ–į–≥–į–∑–ł–Ĺ, –ļ—ä–ī–Ķ—ā–ĺ –Ņ—ä—ā–Ķ—ą–Ķ—Ā—ā–≤–Ķ–Ĺ–ł–ļ—ä—ā –≤—ä–≤ –≤—Ä–Ķ–ľ–Ķ—ā–ĺ —Ź –ļ—É–Ņ—É–≤–į –ł —Ź –Ņ–ĺ–ī–į—Ä—Ź–≤–į –Ĺ–į –®–Ķ–ļ—Ā–Ņ–ł—Ä, –ļ–ĺ–Ļ—ā–ĺ –ĺ—ā–Ĺ–ĺ–≤–ĺ —Ź –Ņ—Ä–Ķ–Ņ–ł—Ā–≤–į –ł —ā.–Ĺ.
–í —ā–ĺ–∑–ł —Ā–Ľ—É—á–į–Ļ –ļ–ĺ–≥–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į —Ā—á–ł—ā–į–ľ–Ķ –∑–į –į–≤—ā–ĺ—Ä –Ĺ–į –∑–Ĺ–į–ľ–Ķ–Ĺ–ł—ā–ĺ—ā–ĺ –Ņ—Ä–ĺ–ł–∑–≤–Ķ–ī–Ķ–Ĺ–ł–Ķ? –°–Ľ–Ķ–ī –ļ–į—ā–ĺ –®–Ķ–ļ—Ā–Ņ–ł—Ä —Ź –Ķ –Ņ–ĺ–Ľ—É—á–ł–Ľ –ļ–į—ā–ĺ –ī–į—Ä –ł —Ź –Ķ –Ņ—Ä–Ķ–Ņ–ł—Ā–į–Ľ?
–ü–į—Ä–į–ī–ĺ–ļ—Ā—ä—ā –Ĺ–į –ľ–ĺ–ľ—á–Ķ—ā–ĺ –ł –ľ–ĺ–ľ–ł—á–Ķ—ā–ĺ
–í —ā–Ķ–ĺ—Ä–ł—Ź—ā–į –Ĺ–į –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā–ł—ā–Ķ —ā–ĺ–∑–ł –Ņ–į—Ä–į–ī–ĺ–ļ—Ā —Ā–Ķ –Ĺ–į—Ä–ł—á–į –ĺ—Č–Ķ „–Ē–Ķ—Ü–į—ā–į –Ĺ–į –≥-–Ĺ –°–ľ–ł—ā“ –ł–Ľ–ł „–ü—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā –Ĺ–į –ľ–ł—Ā–ł—Ā –°–ľ–ł—ā“. –ě—ā–Ĺ–į—á–į–Ľ–ĺ –Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į–Ĺ –ĺ—ā –į–ľ–Ķ—Ä–ł–ļ–į–Ĺ—Ā–ļ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –ú–į—Ä—ā–ł–Ĺ –ď–į—Ä–ī–Ĺ—ä—Ä –≤ –Ķ–ī–ł–Ĺ –ĺ—ā –Ī—Ä–ĺ–Ķ–≤–Ķ—ā–Ķ –Ĺ–į Scientific American. –ě—ā—ā–ĺ–≥–į–≤–į –Ĺ–į—Ā–į–ľ —Ā–į –ł–∑–ľ–ł–Ĺ–į–Ľ–ł –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –ī–Ķ—Ā–Ķ—ā–ł–Ľ–Ķ—ā–ł—Ź, –į —É—á–Ķ–Ĺ–ł—ā–Ķ –ĺ—Č–Ķ —Ā–Ņ–ĺ—Ä—Ź—ā –Ĺ–į–ī –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–į, –ļ–į—ā–ĺ —Ā–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ł –Ņ–ĺ–Ĺ–Ķ –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ –Ĺ–Ķ–≥–ĺ–≤–ł —Ä–Ķ—ą–Ķ–Ĺ–ł—Ź. –ü–ĺ–ľ–ł—Ā–Ľ–Ķ—ā–Ķ –Ĺ–į–ī –Ĺ–Ķ–≥–ĺ –ł –ľ–ĺ–∂–Ķ –ī–į –ī–į–ī–Ķ—ā–Ķ –ł –≤–į—ą –≤–į—Ä–ł–į–Ĺ—ā.
–í –Ķ–ī–Ĺ–ĺ —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–ĺ –ł–ľ–į –ī–≤–Ķ –ī–Ķ—Ü–į –ł –Ķ —Ā–ł–≥—É—Ä–Ĺ–ĺ, —á–Ķ –Ķ–ī–Ĺ–ĺ—ā–ĺ –Ķ –ľ–ĺ–ľ—á–Ķ. –ö–į–ļ–≤–į –Ķ –≤–Ķ—Ä–ĺ—Ź—ā–Ĺ–ĺ—Ā—ā—ā–į –≤—ā–ĺ—Ä–ĺ—ā–ĺ –ī–Ķ—ā–Ķ —Ā—ä—Č–ĺ –ī–į –Ķ –ľ–ĺ–ľ—á–Ķ, —ā–ĺ–Ķ—Ā—ā –ļ–ĺ–Ľ–ļ–ĺ —Ā–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł—ā–Ķ? –Ě–į –Ņ—Ä—ä–≤ –Ņ–ĺ–≥–Ľ–Ķ–ī –ĺ—ā–≥–ĺ–≤–ĺ—Ä—ä—ā –Ķ –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–į—Ä–Ķ–Ĺ – 50 –Ĺ–į 50 (—Ā–į–ľ–ĺ –ī–≤–Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł, –Ĺ–į–Ľ–ł?). –ó–į—Č–ĺ—ā–ĺ –≤—Ā–ł—á–ļ–ł —Ā–ľ—Ź—ā–į—ā–Ķ, —á–Ķ –ī–į–Ľ–ł –Ķ –ľ–ĺ–ľ—á–Ķ –ł–Ľ–ł –ľ–ĺ–ľ–ł—á–Ķ —ą–į–Ĺ—Ā—ä—ā –Ķ –Ķ–ī–Ĺ–į–ļ—ä–≤ (–≤—ä–Ņ—Ä–Ķ–ļ–ł —á–Ķ –≥–Ķ–Ĺ–Ķ—ā–ł—á–Ĺ–ĺ –Ĺ–Ķ –Ķ —ā–ĺ—á–Ĺ–ĺ —ā–į–ļ–į).
–ü—Ä–ĺ–Ī–Ľ–Ķ–ľ—ä—ā –Ķ —ā–į–ľ –ĺ–Ī–į—á–Ķ, —á–Ķ –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł—ā–Ķ —Ā–Ķ –ĺ–ļ–į–∑–≤–į—ā –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā –ī–≤–Ķ –∑–į—Ä–į–ī–ł –Ĺ–į—á–ł–Ĺ–į –Ĺ–į –∑–į–ī–į–≤–į–Ĺ–Ķ –Ĺ–į –≤—ä–Ņ—Ä–ĺ—Ā–į –ł –∑–į—Ä–į–ī–ł —É—Ā–Ľ–ĺ–≤–Ĺ–ĺ—Ā—ā–ł—ā–Ķ. –í —Ā–Ķ–ľ–Ķ–Ļ—Ā—ā–≤–į—ā–į —Ā –ī–≤–Ķ –ī–Ķ—Ü–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā–ł—ā–Ķ –ł –Ņ–ĺ—Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā—ā–į –ł–ľ –Ĺ–į –Ņ–ĺ—Ź–≤–į —Ā–į —Ā–Ľ–Ķ–ī–Ĺ–ł—ā–Ķ: –ľ–ĺ–ľ—á–Ķ-–ľ–ĺ–ľ—á–Ķ, –ľ–ĺ–ľ—á–Ķ-–ľ–ĺ–ľ–ł—á–Ķ, –ľ–ĺ–ľ–ł—á–Ķ-–ľ–ĺ–ľ—á–Ķ, –ľ–ĺ–ľ–ł—á–Ķ-–ľ–ĺ–ľ–ł—á–Ķ. –ė–∑–ļ–Ľ—é—á–≤–į–ľ–Ķ –Ņ—ä—Ä–≤–ł—Ź –≤–į—Ä–ł–į–Ĺ—ā, –∑–į—Č–ĺ—ā–ĺ –≤ –Ĺ–Ķ–≥–ĺ –≤–ł–Ĺ–į–≥–ł –Ķ–ī–Ĺ–ĺ—ā–ĺ –ī–Ķ—ā–Ķ –Ķ –ľ–ĺ–ľ—á–Ķ, –Ĺ–ĺ –≤ –ĺ—Ā—ā–į–Ĺ–į–Ľ–ł—ā–Ķ —ā—Ä–ł —Ā–Ľ—É—á–į—Ź –Ĺ—Ź–ľ–į–ľ–Ķ —Ā—ā–ĺ–Ņ—Ä–ĺ—Ü–Ķ–Ĺ—ā–ĺ–≤–į –≥–į—Ä–į–Ĺ—Ü–ł—Ź, —á–Ķ –Ķ–ī–Ĺ–ĺ—ā–ĺ –ī–Ķ—ā–Ķ —Č–Ķ –Ķ –ľ–ĺ–ľ—á–Ķ, –Ĺ–į–Ľ–ł :)
–ź–ļ–ĺ —Ā—ā–Ķ –ĺ–Ī—ä—Ä–ļ–į–Ĺ–ł – –≤–ł–∂—ā–Ķ –ł–∑—ā–ĺ—á–Ĺ–ł–ļ–į –≤ —É–ł–ļ–ł–Ņ–Ķ–ī–ł—Ź
–ü–į—Ä–į–ī–ĺ–ļ—Ā—ä—ā –Ĺ–į –Ė—É—Ä–ī–Ķ–Ĺ
–ě—Č–Ķ –Ķ–ī–Ĺ–į –≥–Ľ–į–≤–ĺ–Ī–Ľ—ä—Ā–ļ–į–Ĺ–ł—Ü–į, –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–į –ĺ—ā –Ī—Ä–ł—ā–į–Ĺ—Ā–ļ–ł—Ź –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ –§–ł–Ľ–ł–Ņ –Ė—É—Ä–ī–Ķ–Ĺ (—Ö–ľ, –ľ–į–Ľ–ļ–ĺ —Ą—Ä–Ķ–Ĺ—Ā–ļ–ĺ –∑–≤—É—á–ł, –į?) –≤ –Ĺ–į—á–į–Ľ–ĺ—ā–ĺ –Ĺ–į –•–• –≤–Ķ–ļ. –Ę–ĺ–Ļ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —Ā—á–ł—ā–į –∑–į –Ķ–ī–ł–Ĺ –ĺ—ā –≤–į—Ä–ł–į–Ĺ—ā–ł—ā–Ķ –Ĺ–į –∑–Ĺ–į–ľ–Ķ–Ĺ–ł—ā–ł—Ź—ā –Ņ–į—Ä–į–ī–ĺ–ļ—Ā –Ĺ–į –Ľ—ä–∂–Ķ—Ü–į.

–ü—Ä–Ķ–ī—Ā—ā–į–≤–Ķ—ā–Ķ —Ā–ł – –ī—ä—Ä–∂–ł—ā–Ķ –≤ —Ä—ä—Ü–Ķ –ļ–į—Ä—ā–ł—á–ļ–į, –Ĺ–į –ļ–ĺ—Ź—ā–ĺ –Ķ –Ĺ–į–Ņ–ł—Ā–į–Ĺ–ĺ „–Ę–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ĺ–Ī—Ä–į—ā–Ĺ–į—ā–į —Ā—ā—Ä–į–Ĺ–į –Ķ –ł—Ā—ā–ł–Ĺ—Ā–ļ–ĺ“. –ě–Ī—Ä—ä—Č–į—ā–Ķ –ļ–į—Ä—ā–ł—á–ļ–į—ā–į, –į —ā–į–ľ –Ņ–ł—ą–Ķ „–Ę–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ—ā–ĺ –Ĺ–į –ĺ–Ī—Ä–į—ā–Ĺ–į—ā–į —Ā—ā—Ä–į–Ĺ–į –Ķ –Ľ—ä–∂–į“. –•–į-—Ö–į! –†–į–∑–Ī–ł—Ä–į—ā–Ķ –Ľ–ł, –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł–Ķ—ā–ĺ –Ķ –Ĺ–į–Ľ–ł—Ü–Ķ. –ź–ļ–ĺ –Ņ—ä—Ä–≤–ĺ—ā–ĺ —ā–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ –Ķ –ł—Ā—ā–ł–Ĺ–į, —ā–ĺ –≤—ā–ĺ—Ä–ĺ—ā–ĺ —Ā—ä—Č–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į –Ķ –ł—Ā—ā–ł–Ĺ–į, –Ĺ–ĺ –Ņ—ä–ļ –≤ —ā–ĺ–∑–ł —Ā–Ľ—É—á–į–Ļ –Ņ—ä—Ä–≤–ĺ—ā–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į –Ķ –Ľ—ä–∂–į!? –ź–ļ–ĺ –Ņ—ä–ļ –Ņ—ä—Ä–≤–į—ā–į —Ā—ā—Ä–į–Ĺ–į –Ĺ–į –ļ–į—Ä—ā–ł—á–ļ–į—ā–į –Ķ –Ľ—ä–∂–į, —ā–ĺ —Ą—Ä–į–∑–į—ā–į –Ĺ–į –≤—ā–ĺ—Ä–į—ā–į —Ā—ä—Č–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ —Ā—á–ł—ā–į –∑–į –Ľ—ä–∂–Ľ–ł–≤–į, –į —ā–ĺ–≤–į –∑–Ĺ–į—á–ł —á–Ķ –Ņ—ä—Ä–≤–ĺ—ā–ĺ —ā–≤—ä—Ä–ī–Ķ–Ĺ–ł–Ķ –ĺ—ā–Ĺ–ĺ–≤–ĺ —Ā–Ķ –Ņ—Ä–Ķ–≤—Ä—ä—Č–į –≤ –ł—Ā—ā–ł–Ĺ–į.
–°–ĺ—Ą–ł–∑–ľ—ä—ā „–ö—Ä–ĺ–ļ–ĺ–ī–ł–Ľ“
–ě—Č–Ķ –Ķ–ī–ł–Ĺ –ł–Ĺ—ā–Ķ—Ä–Ķ—Ā–Ķ–Ĺ –≤–į—Ä–ł–į–Ĺ—ā –Ĺ–į –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–į –Ĺ–į –Ľ—ä–∂–Ķ—Ü–į. –Ě–į –Ī—Ä–Ķ–≥–į –Ĺ–į —Ä–Ķ–ļ–į —Ā—ā–ĺ—Ź—ā –ľ–į–Ļ–ļ–į —Ā –ī–Ķ—ā–Ķ–Ĺ—Ü–Ķ, –į –ļ—ä–ľ —ā—Ź—Ö –Ņ–Ľ—É–≤–į –ļ—Ä–ĺ–ļ–ĺ–ī–ł–Ľ –ł –ĺ—ā–ļ—Ä–į–ī–≤–į –ī–Ķ—ā–Ķ—ā–ĺ. –ě—ā—á–į—Ź–Ĺ–į—ā–į –ľ–į–Ļ–ļ–į –ľ–ĺ–Ľ–ł –≤–Ľ–Ķ—á—É–≥–ĺ—ā–ĺ –ī–į –≤—ä—Ä–Ĺ–Ķ –ī–Ķ—ā–Ķ—ā–ĺ –Ļ, –Ĺ–į –ļ–ĺ–Ķ—ā–ĺ –ļ—Ä–ĺ–ļ–ĺ–ī–ł–Ľ—ä—ā –ĺ—ā–≥–ĺ–≤–į—Ä—Ź —á–Ķ –Ķ —Ā—ä–≥–Ľ–į—Ā–Ķ–Ĺ –ī–į –≥–ĺ –≤—ä—Ä–Ĺ–Ķ —Ü—Ź–Ľ–ĺ –ł –Ĺ–Ķ–≤—Ä–Ķ–ī–ł–ľ–ĺ, –į–ļ–ĺ –∂–Ķ–Ĺ–į—ā–į –Ņ—Ä–į–≤–ł–Ľ–Ĺ–ĺ –ĺ—ā–≥–ĺ–≤–ĺ—Ä–ł –Ĺ–į –Ĺ–Ķ–≥–ĺ–≤–ł—Ź –≤—ä–Ņ—Ä–ĺ—Ā: „–©–Ķ –≤—ä—Ä–Ĺ–Ķ –Ľ–ł —ā–ĺ–Ļ –ī–Ķ—ā–Ķ—ā–ĺ?“
–Į—Ā–Ĺ–ĺ –Ķ, —á–Ķ –∑–į –∂–Ķ–Ĺ–į—ā–į –ł–ľ–į –ī–≤–į –ĺ—ā–≥–ĺ–≤–ĺ—Ä–į – –ī–į –ł–Ľ–ł –Ĺ–Ķ. –ź–ļ–ĺ —ā—Ź –Ņ–ĺ—ā–≤—ä—Ä–ī–ł, —á–Ķ –ļ—Ä–ĺ–ļ–ĺ–ī–ł–Ľ—ä—ā —Č–Ķ –ł –≤—ä—Ä–Ĺ–Ķ –ī–Ķ—ā–Ķ—ā–ĺ, —ā–ĺ –≤—Ā–ł—á–ļ–ĺ –∑–į–≤–ł—Ā–ł –ĺ—ā –∂–ł–≤–ĺ—ā–Ĺ–ĺ—ā–ĺ – –ī–į–Ľ–ł —ā–ĺ —Č–Ķ —Ä–Ķ—ą–ł –ĺ—ā–≥–ĺ–≤–ĺ—Ä—ä—ā –∑–į –Ņ—Ä–į–≤–ł–Ľ–Ķ–Ĺ. –ź–ļ–ĺ —Ä–Ķ—ą–ł, —á–Ķ –Ķ, —ā–ĺ–≥–į–≤–į –≤—Ä—ä—Č–į –ī–Ķ—ā–Ķ—ā–ĺ, –Ĺ–ĺ –į–ļ–ĺ —Ä–Ķ—ą–ł, —á–Ķ –Ĺ–Ķ –Ķ – —ā—Ź –Ņ–ĺ–≤–Ķ—á–Ķ –Ĺ—Ź–ľ–į –ī–į –≥–ĺ –≤–ł–ī–ł.

–ě—ā—Ä–ł—Ü–į—ā–Ķ–Ľ–Ĺ–ł—Ź—ā –ĺ—ā–≥–ĺ–≤–ĺ—Ä –Ĺ–į –ľ–į–Ļ–ļ–į—ā–į —É—Ā–Ľ–ĺ–∂–Ĺ—Ź–≤–į –ĺ—Č–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ —Ā–ł—ā—É–į—Ü–ł—Ź—ā–į. –ź–ļ–ĺ —ā–ĺ–Ļ —Ā–Ķ –ĺ–ļ–į–∂–Ķ –≤–Ķ—Ä–Ĺ–ł—Ź—ā –Ņ–ĺ—Ö–ł—ā–ł—ā–Ķ–Ľ—Ź—ā —ā—Ä—Ź–Ī–≤–į –ī–į –ł–∑–Ņ—ä–Ľ–Ĺ–ł —É—Ā–Ľ–ĺ–≤–ł–Ķ—ā–ĺ –Ĺ–į —Ā–ī–Ķ–Ľ–ļ–į—ā–į –ł –ī–į –Ņ—É—Ā–Ĺ–Ķ –ī–Ķ—ā–Ķ—ā–ĺ, –Ĺ–ĺ –Ņ–ĺ —ā–ĺ–∑–ł –Ĺ–į—á–ł–Ĺ –ĺ—ā–≥–ĺ–≤–ĺ—Ä—ä—ā –Ĺ–į –ľ–į–Ļ–ļ–į—ā–į –Ĺ—Ź–ľ–į –ī–į –ĺ—ā–≥–ĺ–≤–į—Ä—Ź –Ĺ–į –ī–Ķ–Ļ—Ā—ā–≤–ł—ā–Ķ–Ľ–Ĺ–ĺ—Ā—ā—ā–į. –ó–į –ī–į –ĺ–Ī–Ķ–∑–Ņ–Ķ—á–ł –Ľ—ä–∂–Ľ–ł–≤–ĺ—Ā—ā—ā–į –Ĺ–į —ā–į–ļ—ä–≤ –ĺ—ā–≥–ĺ–≤–ĺ—Ä, –ļ—Ä–ĺ–ļ–ĺ–ī–ł–Ľ—ä—ā —ā—Ä—Ź–Ī–≤–į –ī–į –≤—ä—Ä–Ĺ–Ķ –ī–Ķ—ā–Ķ—ā–ĺ –Ĺ–į –ľ–į–Ļ–ļ–į—ā–į, –Ĺ–ĺ —ā–ĺ–≤–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł –Ĺ–į –ī–ĺ–≥–ĺ–≤–ĺ—Ä–į, –∑–į—Č–ĺ—ā–ĺ –Ĺ–Ķ–Ļ–Ĺ–į—ā–į –≥—Ä–Ķ—ą–ļ–į –Ī–ł —ā—Ä—Ź–Ī–≤–į–Ľ–ĺ –ī–į –ĺ—Ā—ā–į–≤–ł –ī–Ķ—ā–Ķ—ā–ĺ –ł –∑–į–≤–ł–Ĺ–į–≥–ł –Ņ—Ä–ł –ļ—Ä–ĺ–ļ–ĺ–ī–ł–Ľ–į.
–ź–ļ–ĺ —Ā—ā–Ķ —Ā–Ķ –ĺ–Ī—ä—Ä–ļ–į–Ľ–ł, —Ā–Ņ–ĺ–ļ–ĺ–Ļ–Ĺ–ĺ – —Ā–ī–Ķ–Ľ–ļ–į—ā–į –Ņ—Ä–Ķ–ī–Ľ–ĺ–∂–Ķ–Ĺ–į –ĺ—ā –ļ—Ä–ĺ–ļ–ĺ–ī–ł–Ľ–į —Ā—ä–ī—ä—Ä–∂–į –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł–Ķ, –∑–į—ā–ĺ–≤–į –Ĺ–Ķ–≥–ĺ–≤–ĺ—ā–ĺ –ĺ–Ī–Ķ—Č–į–Ĺ–ł–Ķ –Ķ –Ĺ–Ķ–ł–∑–Ņ—ä–Ľ–Ĺ–ł–ľ–ĺ. –ó–į –į–≤—ā–ĺ—Ä –Ĺ–į —ā–ĺ–∑–ł –ļ–Ľ–į—Ā–ł—á–Ķ—Ā–ļ–ł —Ā–ĺ—Ą–ł–∑—ä–ľ (–ī—É–ľ–į, –ľ–ł—Ā—ä–Ľ, –ł–∑–ļ–į–∑–≤–į–Ĺ–Ķ, –ļ–ĺ—Ź—ā–ĺ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į –Ľ—ä–∂–Ľ–ł–≤ –į—Ä–≥—É–ľ–Ķ–Ĺ—ā) —Ā–Ķ —Ā—á–ł—ā–į –ĺ—Ä–į—ā–ĺ—Ä—ä—ā –ł —Ą–ł–Ľ–ĺ—Ā–ĺ—Ą –ö–ĺ—Ä–į–ļ—Ā –ĺ—ā –°–ł—Ä–į–ļ—É–∑–į, –∂–ł–≤—Ź–Ľ –Ņ—Ä–Ķ–∑ V –≤–Ķ–ļ –Ņ—Ä–Ķ–ī–ł –Ĺ–ĺ–≤–į—ā–į –Ķ—Ä–į.
–í—Ä–Ķ–ľ–Ķ –∑–į –Ī–Ķ—Ā–ł–Ľ–ļ–į
–°—ä–ī–ł—Ź –Ņ–ĺ—Ā—ā–į–Ĺ–ĺ–≤—Ź–≤–į –Ņ—Ä–ł—Ā—ä–ī–į—ā–į —Ā–ł – –∑–į—ā–≤–ĺ—Ä–Ĺ–ł–ļ—ä—ā —Č–Ķ –Ī—ä–ī–Ķ –ĺ–Ī–Ķ—Ā–Ķ–Ĺ –Ņ–ĺ –ĺ–Ī—Ź–ī –≤ –Ĺ—Ź–ļ–ĺ–Ļ –ī–Ķ–Ľ–Ĺ–ł—á–Ķ–Ĺ –ī–Ķ–Ĺ –Ņ—Ä–Ķ–∑ —Ā–Ľ–Ķ–ī–≤–į—Č–į—ā–į —Ā–Ķ–ī–ľ–ł—Ü–į, –Ĺ–ĺ –Ķ–ļ–∑–Ķ–ļ—É—Ü–ł—Ź—ā–į —Č–Ķ –Ī—ä–ī–Ķ –ł–∑–Ĺ–Ķ–Ĺ–į–ī–į –∑–į –ĺ—Ā—ä–ī–Ķ–Ĺ–ł—Ź. –Ę–ĺ–Ļ –Ĺ—Ź–ľ–į –ī–į —É–∑–Ĺ–į–Ķ –ī–Ķ–Ĺ—Ź –Ĺ–į –Ķ–ļ–∑–Ķ–ļ—É—Ü–ł—Ź—ā–į —Ā–ł –ī–ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā–į, –≤ –ļ–ĺ–Ļ—ā–ĺ –Ķ–ļ–∑–Ķ–ļ—É—ā–ĺ—Ä—ä—ā –Ĺ–Ķ –Ņ–ĺ—á—É–ļ–į –Ĺ–į –≤—Ä–į—ā–į—ā–į –Ĺ–į –ļ–ł–Ľ–ł—Ź—ā–į –Ņ–ĺ –ĺ–Ī—Ź–ī –≤—ä–≤ —Ą–į—ā–į–Ľ–Ĺ–ł—Ź –ī–Ķ–Ĺ.

–°–Ľ–Ķ–ī–≤–į–Ļ–ļ–ł –Ľ–ĺ–≥–ł–ļ–į—ā–į –Ĺ–į –Ņ—Ä–ł—Ā—ä–ī–į—ā–į —Ā–ł, –∑–į—ā–≤–ĺ—Ä–Ĺ–ł–ļ—ä—ā —ā—Ä—Ź–Ī–≤–į –ī–į –Ī—ä–ī–Ķ —Ā–Ņ–ĺ–ļ–ĺ–Ķ–Ĺ, —á–Ķ… –Ĺ–ł–ļ–ĺ–≥–į –Ĺ—Ź–ľ–į –ī–į –Ī—ä–ī–Ķ –ĺ–Ī–Ķ—Ā–Ķ–Ĺ. –ó–į—Č–ĺ –Ľ–ł? –Ě–Ķ–≥–ĺ–≤–į—ā–į –Ľ–ĺ–≥–ł–ļ–į —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā –Ĺ—Ź–ļ–ĺ–Ľ–ļ–ĺ —á–į—Ā—ā–ł. –†–į–∑—Ā—ä–∂–ī–Ķ–Ĺ–ł—Ź—ā–į –∑–į–Ņ–ĺ—á–≤–į—ā –ĺ—ā—ā–į–ľ, —á–Ķ „–ł–∑–Ĺ–Ķ–Ĺ–į–ī–≤–į—Č–ĺ—ā–ĺ –ĺ–Ī–Ķ—Ā–≤–į–Ĺ–Ķ“ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –≤ –Ņ–Ķ—ā—ä–ļ, –∑–į—Č–ĺ—ā–ĺ, –į–ļ–ĺ –Ķ —ā–ĺ–≥–į–≤–į, —ā–ĺ–Ļ —Č–Ķ –≥–ĺ –Ķ —É–∑–Ĺ–į–Ľ –ĺ—Č–Ķ —Ā–Ľ–Ķ–ī –ļ–į—ā–ĺ –Ķ –ľ–ł–Ĺ–į–Ľ–ĺ –ĺ–Ī–Ķ–ī–Ĺ–ĺ—ā–ĺ –≤—Ä–Ķ–ľ–Ķ –Ĺ–į –Ņ—Ä–Ķ–ī–Ĺ–ł—Ź—ā –ī–Ķ–Ĺ – —á–Ķ—ā–≤—ä—Ä—ā—ä–ļ. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ –Ĺ—Ź–ľ–į –ī–į –Ķ –ł–∑–Ĺ–Ķ–Ĺ–į–ī–į –ł –Ņ–Ķ—ā—ä–ļ–į –ĺ—ā–Ņ–į–ī–į. –õ–ĺ–≥–ł–ļ–į—ā–į –Ĺ–į –ľ–ł—Ā—ä–Ľ—ā–į –Ņ—Ä–ĺ–ī—ä–Ľ–∂–į–≤–į –ł –ł–∑–Ľ–ł–∑–į, —á–Ķ –ĺ–Ī–Ķ—Ā–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –ł –≤ —á–Ķ—ā–≤—ä—Ä—ā—ä–ļ, –∑–į—Č–ĺ—ā–ĺ –Ņ–Ķ—ā—ä–ļ –≤–Ķ—á–Ķ –Ķ –Ķ–Ľ–ł–ľ–ł–Ĺ–ł—Ä–į–Ĺ –ł –į–ļ–ĺ —ā–ĺ–Ļ –Ĺ–Ķ –Ķ –≤–Ķ—á–Ķ –ĺ–Ī–Ķ—Ā–Ķ–Ĺ –≤ —á–Ķ—ā–≤—ä—Ä—ā—ä–ļ –≤–Ķ—á–Ķ—Ä, –ĺ–Ī–Ķ—Ā–≤–į–Ĺ–Ķ—ā–ĺ —ā—Ä—Ź–Ī–≤–į –ī–į –Ķ –≤ —Ā—Ä—Ź–ī–į, –ļ–ĺ–Ķ—ā–ĺ –Ņ—ä–ļ –ĺ—ā—Ā—ā—Ä–į–Ĺ—Ź–≤–į –ł–∑–Ĺ–Ķ–Ĺ–į–ī–į—ā–į –ĺ—ā —É–≤–ł—Ā–≤–į–Ĺ–Ķ—ā–ĺ –Ĺ–į –≤—ä–∂–Ķ—ā–ĺ –≤ —á–Ķ—ā–≤—ä—Ä—ā—ä–ļ. –ü–ĺ —Ā—ä—Č–į—ā–į –Ľ–ĺ–≥–ł–ļ–į –ĺ—ā–Ņ–į–ī–į—ā –≤—Ā–ł—á–ļ–ł –ī–Ķ–Ľ–Ĺ–ł—á–Ĺ–ł –ī–Ĺ–ł. –ė —ā–į–ļ–į –∑–į—ā–≤–ĺ—Ä–Ĺ–ł–ļ—ä—ā —Ā–Ņ–ĺ–ļ–ĺ–Ļ–Ĺ–ĺ —Ā–Ķ –Ņ—Ä–ł–Ī–ł—Ä–į –≤ –ļ–ł–Ľ–ł—Ź—ā–į —Ā–ł, —Ä–į–ī–≤–į–Ļ–ļ–ł —Ā–Ķ, —á–Ķ –Ĺ–ł–ļ–ĺ–≥–į –Ĺ—Ź–ľ–į –ī–į –Ī—ä–ī–Ķ –ĺ–Ī–Ķ—Ā–Ķ–Ĺ…
–ü—Ä–Ķ–∑ —Ā–Ľ–Ķ–ī–≤–į—Č–į—ā–į —Ā–Ķ–ī–ľ–ł—Ü–į, –≤ —á–Ķ—ā–≤—ä—Ä—ā—ä–ļ –Ņ–ĺ –ĺ–Ī—Ź–ī, —Ā–Ņ–ĺ–ļ–ĺ–Ļ—Ā—ā–≤–ł–Ķ—ā–ĺ –Ĺ–į –Ľ–Ķ–∂–į—Č–ł—Ź –≤ –ļ–ł–Ľ–ł—Ź—ā–į –∑–į—ā–≤–ĺ—Ä–Ĺ–ł–ļ –Ķ –Ĺ–į—Ä—É—ą–Ķ–Ĺ–ĺ. –Ě–į –≤—Ä–į—ā–į—ā–į –Ņ–ĺ—á—É–ļ–≤–į –Ķ–ļ–∑–Ķ–ļ—É—ā–ĺ—Ä—ä—ā. –°–ł–≥—É—Ä–Ĺ–ł—Ź—ā –≤ –Ľ–ĺ–≥–ł–ļ–į—ā–į —Ā–ł –ĺ—Ā—ä–ī–Ķ–Ĺ –Ķ… –Ĺ–į–ł—Ā—ā–ł–Ĺ–į –ł–∑–Ĺ–Ķ–Ĺ–į–ī–į–Ĺ, –į —Ā—ä–ī–ł—Ź—ā–į –Ķ —Ā–Ņ–į–∑–ł–Ľ –ĺ–Ī–Ķ—Č–į–Ĺ–ł–Ķ—ā–ĺ —Ā–ł. –°–Ķ—Č–į—ā–Ķ –Ľ–ł —Ā–Ķ?
–ź–Ņ–ĺ—Ä–ł—Ź—ā–į „–Ľ–Ķ—ā—Ź—Č–į —Ā—ā—Ä–Ķ–Ľ–į“
–ó–Ĺ–į–ľ–Ķ–Ĺ–ł—ā–ł—Ź—ā –Ņ–į—Ä–į–ī–ĺ–ļ—Ā –Ĺ–į –ó–Ķ–Ĺ–ĺ–Ĺ –ĺ—ā –ē–Ľ–Ķ—Ź –Ņ–ĺ–ļ–į–∑–≤–į –ĺ–≥—Ä–ĺ–ľ–Ĺ–ł—ā–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł—Ź –≤ –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–ł—ā–Ķ –Ĺ–į —É—á–Ķ–Ĺ–ł—ā–Ķ –∑–į –≤—Ä–Ķ–ľ–Ķ –ł –ī–≤–ł–∂–Ķ–Ĺ–ł–Ķ. –ē—ā–ĺ –ł —ā–ĺ–∑–ł –Ņ–į—Ä–į–ī–ĺ–ļ—Ā: —Ā—ā—Ä–Ķ–Ľ–į, –Ņ—É—Ā–Ĺ–į—ā–į –ĺ—ā –Ľ—ä–ļ, 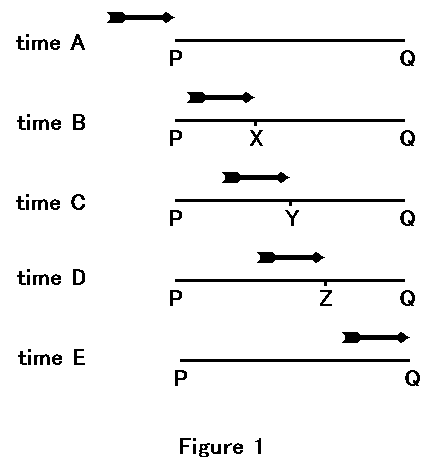 –Ĺ–į –Ņ—Ä–į–ļ—ā–ł–ļ–į –Ī–ł —ā—Ä—Ź–Ī–≤–į–Ľ–ĺ –ī–į –Ķ –∑–į–ľ—Ä—ä–∑–Ĺ–į–Ľ–į –≤—ä–≤ –≤—ä–∑–ī—É—Ö–į –ł –ī–į –Ĺ–Ķ —Ā–Ķ –ī–≤–ł–∂–ł, –∑–į—Č–ĺ—ā–ĺ, —Ä–į–∑–≥–Ľ–Ķ–ī–į–Ĺ–ĺ –≤ –ī–į–ī–Ķ–Ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā –ĺ—ā –≤—Ä–Ķ–ľ–Ķ—ā–ĺ, –Ĺ–Ķ–Ļ–Ĺ–ĺ—ā–ĺ –ľ–Ķ—Ā—ā–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ķ —ā–ĺ—á–Ĺ–ĺ –ł –∑–į–ļ–ĺ–≤–į–Ĺ–ĺ —Ā–Ņ–ĺ—Ä–Ķ–ī –≥–Ľ–Ķ–ī–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ. –Ě–ĺ –į–ļ–ĺ —ā–ĺ–≤–į –Ķ —ā–į–ļ–į –ł –≤ –ī–į–ī–Ķ–Ĺ –≤—Ä–Ķ–ľ–Ķ–≤–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā —ā—Ź –Ķ –Ĺ–į –ł–ī–Ķ–į–Ľ–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–ľ–į –Ņ–ĺ–∑–ł—Ü–ł—Ź, —ā–ĺ –∑–Ĺ–į—á–ł —ā—Ź –≤–ł–Ĺ–į–≥–ł —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į –≤ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ĺ–į –Ņ–ĺ–ļ–ĺ–Ļ –ł –Ĺ–Ķ —Ā–Ķ –ī–≤–ł–∂–ł –ł–∑–ĺ–Ī—Č–ĺ!
–Ĺ–į –Ņ—Ä–į–ļ—ā–ł–ļ–į –Ī–ł —ā—Ä—Ź–Ī–≤–į–Ľ–ĺ –ī–į –Ķ –∑–į–ľ—Ä—ä–∑–Ĺ–į–Ľ–į –≤—ä–≤ –≤—ä–∑–ī—É—Ö–į –ł –ī–į –Ĺ–Ķ —Ā–Ķ –ī–≤–ł–∂–ł, –∑–į—Č–ĺ—ā–ĺ, —Ä–į–∑–≥–Ľ–Ķ–ī–į–Ĺ–ĺ –≤ –ī–į–ī–Ķ–Ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā –ĺ—ā –≤—Ä–Ķ–ľ–Ķ—ā–ĺ, –Ĺ–Ķ–Ļ–Ĺ–ĺ—ā–ĺ –ľ–Ķ—Ā—ā–ĺ–Ņ–ĺ–Ľ–ĺ–∂–Ķ–Ĺ–ł–Ķ –Ķ —ā–ĺ—á–Ĺ–ĺ –ł –∑–į–ļ–ĺ–≤–į–Ĺ–ĺ —Ā–Ņ–ĺ—Ä–Ķ–ī –≥–Ľ–Ķ–ī–Ĺ–į—ā–į —ā–ĺ—á–ļ–į –Ĺ–į –ľ–į—ā–Ķ–ľ–į—ā–ł—Ü–ł—ā–Ķ. –Ě–ĺ –į–ļ–ĺ —ā–ĺ–≤–į –Ķ —ā–į–ļ–į –ł –≤ –ī–į–ī–Ķ–Ĺ –≤—Ä–Ķ–ľ–Ķ–≤–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā —ā—Ź –Ķ –Ĺ–į –ł–ī–Ķ–į–Ľ–Ĺ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–ł–ľ–į –Ņ–ĺ–∑–ł—Ü–ł—Ź, —ā–ĺ –∑–Ĺ–į—á–ł —ā—Ź –≤–ł–Ĺ–į–≥–ł —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į –≤ –ĺ—ā–Ĺ–ĺ—Ā–ł—ā–Ķ–Ľ–Ĺ–ĺ —Ā—ä—Ā—ā–ĺ—Ź–Ĺ–ł–Ķ –Ĺ–į –Ņ–ĺ–ļ–ĺ–Ļ –ł –Ĺ–Ķ —Ā–Ķ –ī–≤–ł–∂–ł –ł–∑–ĺ–Ī—Č–ĺ!
–ď–ĺ–Ľ–Ķ–ľ–ł—ā–Ķ —É–ľ–ĺ–≤–Ķ –ĺ—ā –≤–Ķ–ļ–ĺ–≤–Ķ –ĺ–Ņ–ł—ā–≤–į—ā –ī–į —Ä–Ķ—ą–į—ā —ā–ĺ–∑–ł –Ņ–į—Ä–į–ī–ĺ–ļ—Ā, –∑–į—Č–ĺ—ā–ĺ –ĺ—ā –Ľ–ĺ–≥–ł—á–Ķ—Ā–ļ–į –≥–Ľ–Ķ–ī–Ĺ–į —ā–ĺ—á–ļ–į —ā–ĺ–Ļ –Ķ —Ā—ä—Ā—ā–į–≤–Ķ–Ĺ –į–Ī—Ā–ĺ–Ľ—é—ā–Ĺ–ĺ —ā–ĺ—á–Ĺ–ĺ. –ó–į –Ĺ–Ķ–≥–ĺ–≤–ĺ—ā–ĺ –ĺ–Ņ—Ä–ĺ–≤–Ķ—Ä–∂–Ķ–Ĺ–ł–Ķ –Ķ –Ĺ—É–∂–Ĺ–ĺ –ī–į —Ā–Ķ –ĺ–Ī—Ź—Ā–Ĺ–ł –ļ–į–ļ –Ķ–ī–ł–Ĺ –ļ—Ä–į–Ķ–Ĺ –≤—Ä–Ķ–ľ–Ķ–≤–ł –ĺ—ā—Ä—Ź–∑—ä–ļ –ľ–ĺ–∂–Ķ –ī–į —Ā–Ķ —Ā—ä—Ā—ā–ĺ–ł –ĺ—ā –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ –ľ–ĺ–ľ–Ķ–Ĺ—ā–ł. –Ě–į–ī —ā–į–ļ–ĺ–≤–į –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–ĺ —Ā–Ķ –Ķ –ľ—ä—á–ł–Ľ –ī–ĺ—Ä–ł –ź—Ä–ł—Ā—ā–ĺ—ā–Ķ–Ľ –ł –Ĺ–Ķ –Ķ —É—Ā–Ņ—Ź–Ľ. –§–ł–Ľ–ĺ—Ā–ĺ—Ą—ä—ā –Ņ–ĺ—Ā–ĺ—á–≤–į–Ľ, —á–Ķ –ĺ—ā—Ä—Ź–∑—ä–ļ—ä—ā –≤—Ä–Ķ–ľ–Ķ –Ĺ–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ —Ā—á–ł—ā–į –ļ–į—ā–ĺ —Ā—É–ľ–į –ĺ—ā –Ĺ—Ź–ļ–į–ļ–≤–ł –Ĺ–Ķ–ī–Ķ–Ľ–ł–ľ–ł –ł–∑–ĺ–Ľ–ł—Ä–į–Ĺ–ł –ľ–ĺ–ľ–Ķ–Ĺ—ā–ł.
–ė –≤—Ā–Ķ –Ņ–į–ļ –ľ–Ĺ–ĺ–≥–ĺ —É—á–Ķ–Ĺ–ł —Ā—á–ł—ā–į—ā, —á–Ķ –Ņ–ĺ–ī—Ö–ĺ–ī—ä—ā –Ĺ–į –ź—Ä–ł—Ā—ā–ĺ—ā–Ķ–Ľ –Ķ –Ņ–ĺ–≤—ä—Ä—Ö–Ĺ–ĺ—Ā—ā–Ķ–Ĺ –ł –Ĺ–Ķ –ĺ–Ņ—Ä–ĺ–≤–Ķ—Ä–≥–į–≤–į –Ĺ–į–Ľ–ł—á–ł–Ķ—ā–ĺ –Ĺ–į –Ņ–į—Ä–į–ī–ĺ–ļ—Ā. –Ę—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ –ĺ—ā–Ī–Ķ–Ľ–Ķ–∂–ł –ĺ–Ī–į—á–Ķ, —á–Ķ –Ņ–ĺ—Ā–ĺ—á–≤–į–Ļ–ļ–ł —Ā–≤–ĺ–ł—ā–Ķ –Ņ–į—Ä–į–ī–ĺ–ļ—Ā–ł, –ó–Ķ–Ĺ–ĺ–Ĺ –Ĺ–Ķ –Ķ –ł—Ā–ļ–į–Ľ –ī–į –ĺ–Ņ—Ä–ĺ–≤–Ķ—Ä–≥–į–≤–į –≤—ä–∑–ľ–ĺ–∂–Ĺ–ĺ—Ā—ā—ā–į –∑–į –ī–≤–ł–∂–Ķ–Ĺ–ł–Ķ—ā–ĺ —Ā–į–ľ–ĺ –Ņ–ĺ —Ā–Ķ–Ī–Ķ —Ā–ł, –į –Ņ–ĺ-—Ā–ļ–ĺ—Ä–ĺ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł—Ź—ā–į –≤ –ł–ī–Ķ–į–Ľ–ł—Ā—ā–ł—á–Ĺ–ł—ā–Ķ –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –≤—ä–∑–≥–Ľ–Ķ–ī–ł.
–ü–į—Ä–į–ī–ĺ–ļ—Ā—ä—ā –Ĺ–į –ď–į–Ľ–ł–Ľ–Ķ–Ļ
–í —Ā–≤–ĺ—Ź —ā—Ä—É–ī „–Ď–Ķ—Ā–Ķ–ī–ł –ł –ľ–į—ā–Ķ–ľ–į—ā–ł—á–Ķ—Ā–ļ–ł –ī–ĺ–ļ–į–∑–į—ā–Ķ–Ľ—Ā—ā–≤–į –ĺ—ā–Ĺ–ĺ—Ā–Ĺ–ĺ –ī–≤–Ķ –Ĺ–ĺ–≤–ł –Ĺ–į–Ņ—Ä–į–≤–Ľ–Ķ–Ĺ–ł—Ź –Ĺ–į –Ĺ–į—É–ļ–į—ā–į“  –ď–į–Ľ–ł–Ľ–Ķ–ĺ –ď–į–Ľ–ł–Ľ–Ķ–Ļ –Ņ—Ä–Ķ–ī–Ľ–į–≥–į –Ņ–į—Ä–į–ī–ĺ–ļ—Ā, –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–į—Č –Ľ—é–Ī–ĺ–Ņ–ł—ā–Ĺ–ł—ā–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ĺ–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ł—ā–Ķ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į. –£—á–Ķ–Ĺ–ł—Ź—ā —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į –ī–≤–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–į—Č–ł –Ķ–ī–Ĺ–ĺ –Ĺ–į –ī—Ä—É–≥–ĺ —Ā—ä–∂–ī–Ķ–Ĺ–ł—Ź. –ü—ä—Ä–≤–ĺ—ā–ĺ: –ł–ľ–į —á–ł—Ā–Ľ–į, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—Č–ł —Ā—É–ľ–į –Ĺ–į –ļ–≤–į–ī—Ä–į—ā –ĺ—ā –ī—Ä—É–≥–ł —Ü–Ķ–Ľ–ł —á–ł—Ā–Ľ–į – –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä 1, 9, 16, 25, 36 –ł —ā.–Ĺ. –°—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –ł –ī—Ä—É–≥–ł —á–ł—Ā–Ľ–į –Ņ—Ä–ł –ļ–ĺ–ł—ā–ĺ –Ĺ—Ź–ľ–į —ā–į–ļ–ĺ–≤–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ – 2, 3, 5, 6, 7, 8, 10 –ł –ī—Ä. –°–Ņ–ĺ—Ä–Ķ–ī —ā–į–∑–ł –Ľ–ĺ–≥–ł–ļ–į –ĺ–Ī—Č–ł—Ź—ā –Ī—Ä–ĺ–Ļ –Ĺ–į –≤—Ā–ł—á–ļ–ł —ā–ĺ—á–Ĺ–ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł —á–ł—Ā–Ľ–į –ł –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į —ā—Ä—Ź–Ī–≤–į –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ –ĺ—ā –Ī—Ä–ĺ—Ź –Ĺ–į —Ā–į–ľ–ĺ —ā–ĺ—á–Ĺ–ł—ā–Ķ –ļ–≤–į–ī—Ä–į—ā–ł.
–ď–į–Ľ–ł–Ľ–Ķ–ĺ –ď–į–Ľ–ł–Ľ–Ķ–Ļ –Ņ—Ä–Ķ–ī–Ľ–į–≥–į –Ņ–į—Ä–į–ī–ĺ–ļ—Ā, –ī–Ķ–ľ–ĺ–Ĺ—Ā—ā—Ä–ł—Ä–į—Č –Ľ—é–Ī–ĺ–Ņ–ł—ā–Ĺ–ł—ā–Ķ —Ā–≤–ĺ–Ļ—Ā—ā–≤–į –Ĺ–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ł—ā–Ķ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į. –£—á–Ķ–Ĺ–ł—Ź—ā —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į –ī–≤–Ķ –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–į—Č–ł –Ķ–ī–Ĺ–ĺ –Ĺ–į –ī—Ä—É–≥–ĺ —Ā—ä–∂–ī–Ķ–Ĺ–ł—Ź. –ü—ä—Ä–≤–ĺ—ā–ĺ: –ł–ľ–į —á–ł—Ā–Ľ–į, –Ņ—Ä–Ķ–ī—Ā—ā–į–≤–Ľ—Ź–≤–į—Č–ł —Ā—É–ľ–į –Ĺ–į –ļ–≤–į–ī—Ä–į—ā –ĺ—ā –ī—Ä—É–≥–ł —Ü–Ķ–Ľ–ł —á–ł—Ā–Ľ–į – –Ĺ–į–Ņ—Ä–ł–ľ–Ķ—Ä 1, 9, 16, 25, 36 –ł —ā.–Ĺ. –°—ä—Č–Ķ—Ā—ā–≤—É–≤–į—ā –ł –ī—Ä—É–≥–ł —á–ł—Ā–Ľ–į –Ņ—Ä–ł –ļ–ĺ–ł—ā–ĺ –Ĺ—Ź–ľ–į —ā–į–ļ–ĺ–≤–į —Ā–≤–ĺ–Ļ—Ā—ā–≤–ĺ – 2, 3, 5, 6, 7, 8, 10 –ł –ī—Ä. –°–Ņ–ĺ—Ä–Ķ–ī —ā–į–∑–ł –Ľ–ĺ–≥–ł–ļ–į –ĺ–Ī—Č–ł—Ź—ā –Ī—Ä–ĺ–Ļ –Ĺ–į –≤—Ā–ł—á–ļ–ł —ā–ĺ—á–Ĺ–ł –ļ–≤–į–ī—Ä–į—ā–Ĺ–ł —á–ł—Ā–Ľ–į –ł –ĺ–Ī–ł–ļ–Ĺ–ĺ–≤–Ķ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į —ā—Ä—Ź–Ī–≤–į –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ-–≥–ĺ–Ľ—Ź–ľ –ĺ—ā –Ī—Ä–ĺ—Ź –Ĺ–į —Ā–į–ľ–ĺ —ā–ĺ—á–Ĺ–ł—ā–Ķ –ļ–≤–į–ī—Ä–į—ā–ł.
–í—ā–ĺ—Ä–ĺ—ā–ĺ —Ā—ä–∂–ī–Ķ–Ĺ–ł–Ķ: –∑–į –≤—Ā—Ź–ļ–ĺ –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ĺ —á–ł—Ā–Ľ–ĺ —Ā–Ķ –Ĺ–į–ľ–ł—Ä–į –Ĺ–Ķ–≥–ĺ–≤ —ā–ĺ—á–Ķ–Ĺ –ļ–≤–į–ī—Ä–į—ā, –į –∑–į –≤—Ā–Ķ–ļ–ł –ļ–≤–į–ī—Ä–į—ā —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į —Ü—Ź–Ľ –ļ–≤–į–ī—Ä–į—ā–Ķ–Ĺ –ļ–ĺ—Ä–Ķ–Ĺ, —ā–į–ļ–į —á–Ķ –Ī—Ä–ĺ—Ź—ā –Ĺ–į –ļ–≤–į–ī—Ä–į—ā–ł—ā–Ķ –Ķ —Ä–į–≤–Ķ–Ĺ –Ĺ–į –Ī—Ä–ĺ—Ź—ā –Ĺ–į –Ķ—Ā—ā–Ķ—Ā—ā–≤–Ķ–Ĺ–ł—ā–Ķ —á–ł—Ā–Ľ–į.
–í—ä–∑ –ĺ—Ā–Ĺ–ĺ–≤–į –Ĺ–į —ā–ĺ–≤–į –Ņ—Ä–ĺ—ā–ł–≤–ĺ—Ä–Ķ—á–ł–Ķ –ď–į–Ľ–ł–Ľ–Ķ–Ļ –Ņ—Ä–į–≤–ł –ł–∑–≤–ĺ–ī–į, —á–Ķ —Ä–į–∑—Ā—ä–∂–ī–Ķ–Ĺ–ł—Ź—ā–į –∑–į –Ī—Ä–ĺ—Ź –Ĺ–į –Ķ–Ľ–Ķ–ľ–Ķ–Ĺ—ā–ł—ā–Ķ —Ā–į –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–ł —Ā–į–ľ–ĺ –ļ—ä–ľ –ļ—Ä–į–Ļ–Ĺ–ł –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į, –ľ–į–ļ–į—Ä —á–Ķ –≥–ĺ–ī–ł–Ĺ–ł –Ņ–ĺ-–ļ—ä—Ā–Ĺ–ĺ –≤ –ľ–į—ā–Ķ–ľ–į—ā–ł–ļ–į—ā–į –Ķ –≤—ä–≤–Ķ–ī–Ķ–Ĺ–ĺ –Ņ–ĺ–Ĺ—Ź—ā–ł–Ķ—ā–ĺ „–ľ–ĺ—Č–Ĺ–ĺ—Ā—ā –Ĺ–į –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į—ā–į“, —Ā –Ņ–ĺ–ľ–ĺ—Č—ā–į –Ĺ–į –ļ–ĺ–Ķ—ā–ĺ –Ķ –ī–ĺ–ļ–į–∑–į–Ĺ–į –≤–Ķ—Ä–Ĺ–ĺ—Ā—ā—ā–į –Ĺ–į –≤—ā–ĺ—Ä–ĺ—ā–ĺ —Ā—ä–∂–ī–Ķ–Ĺ–ł–Ķ –Ĺ–į –ď–į–Ľ–ł–Ľ–Ķ–Ļ –ł –∑–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ł—ā–Ķ –ľ–Ĺ–ĺ–∂–Ķ—Ā—ā–≤–į.
–ü–į—Ä–į–ī–ĺ–ļ—Ā—ä—ā –Ĺ–į –Ī—Ä—ä—Ā–Ĺ–į—Ä—Ź
–ü—Ä–Ķ–ī—Ā—ā–į–≤–Ķ—ā–Ķ —Ā–ł –≥—Ä–į–ī —Ā –Ĺ–Ķ—É–ľ–ĺ–Ľ–ł–ľ–ł –Ņ—Ä–į–≤–ł–Ľ–į, –≤ –ļ–ĺ–Ļ—ā–ĺ –∂–ł–≤–Ķ–Ķ —Ā–į–ľ–ĺ –Ķ–ī–ł–Ĺ –ľ—ä–∂ –Ī—Ä—ä—Ā–Ĺ–į—Ä, –į –≤—Ā–Ķ–ļ–ł –ľ—ä–∂ –≤ –≥—Ä–į–ī–į —Ā–Ķ –Ņ–ĺ–ī–ī—ä—Ä–∂–į –Ķ–∂–Ķ–ī–Ĺ–Ķ–≤–Ĺ–ĺ –≥–Ľ–į–ī–ļ–ĺ –ł–∑–Ī—Ä—ä—Ā–Ĺ–į—ā. –ē–ī–Ĺ–į —á–į—Ā—ā –ĺ—ā –ľ—ä–∂–Ķ—ā–Ķ —Ā–Ķ –Ī—Ä—ä—Ā–Ĺ–į—ā —Ā–į–ľ–ł, –į –ī—Ä—É–≥–į—ā–į —á–į—Ā—ā –Ņ–ĺ—Ā–Ķ—Č–į–≤–į—ā –Ī—Ä—ä—Ā–Ĺ–į—Ä—Ź. –ė–∑–≥–Ľ–Ķ–∂–ī–į –ī–ĺ—Ā—ā–į –Ņ—Ä–ĺ—Ā—ā–ĺ –ł –Ľ–ĺ–≥–ł—á–Ĺ–ĺ –ł —ā–ĺ–Ļ —Ā–Ľ–Ķ–ī–≤–į –Ĺ–Ķ—É–ľ–ĺ–Ľ–ł–ľ–ĺ—ā–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ „–Ď—Ä—ä—Ā–Ĺ–į—Ä—Ź—ā –Ī—Ä—ä—Ā–Ĺ–Ķ —Ā–į–ľ–ĺ –ĺ–Ĺ–Ķ–∑–ł –ľ—ä–∂–Ķ –≤ –≥—Ä–į–ī–į, –ļ–ĺ–ł—ā–ĺ –Ĺ–Ķ —Ā–Ķ –Ī—Ä—ä—Ā–Ĺ–į—ā —Ā–į–ľ–ł“.

–°–Ľ–Ķ–ī–≤–į–Ļ–ļ–ł —ā–į–∑–ł –Ľ–ĺ–≥–ł–ļ–į –Ĺ–Ķ–ļ–į –∑–į–ī–į–ī–Ķ–ľ —Ā–Ľ–Ķ–ī–Ĺ–ł—Ź –≤—ä–Ņ—Ä–ĺ—Ā: –ź –ī–į–Ľ–ł –Ī—Ä—ä—Ā–Ĺ–į—Ä—Ź—ā —Ā–Ķ –Ī—Ä—ä—Ā–Ĺ–Ķ —Ā–į–ľ? –ó–į–ī–į–≤–į–Ļ–ļ–ł –≤—ä–Ņ—Ä–ĺ—Ā–į, –ĺ—ā–ļ—Ä–ł–≤–į–ľ–Ķ, —á–Ķ —Ā–ł—ā—É–į—Ü–ł—Ź—ā–į –ł–∑–≥–Ľ–Ķ–∂–ī–į –Ĺ–Ķ–≤—ä–∑–ľ–ĺ–∂–Ĺ–į. –ó–į—Č–ĺ –Ľ–ł?
- –ź–ļ–ĺ –Ī—Ä—ä—Ā–Ĺ–į—Ä—Ź—ā –Ĺ–Ķ —Ā–Ķ –Ī—Ä—ä—Ā–Ĺ–Ķ —Ā–į–ľ, —ā–ĺ–Ļ —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ –Ņ–ĺ–ī—á–ł–Ĺ–ł –Ĺ–į –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ –ł –ī–į —Ā–Ķ –ĺ–Ī—Ä—ä—Ā–Ĺ–Ķ —Ā–į–ľ.
- –ź–ļ–ĺ –Ī—Ä—ä—Ā–Ĺ–į—Ä—Ź—ā —Ā–Ķ –Ī—Ä—ä—Ā–Ĺ–Ķ —Ā–į–ľ, —Ā–Ņ–ĺ—Ä–Ķ–ī –Ņ—Ä–į–≤–ł–Ľ–ĺ—ā–ĺ —ā–ĺ–Ļ –Ĺ–Ķ —ā—Ä—Ź–Ī–≤–į –ī–į —Ā–Ķ –Ī—Ä—ä—Ā–Ĺ–Ķ –Ņ–ĺ–≤–Ķ—á–Ķ –ĺ—ā –Ķ–ī–ł–Ĺ –Ņ—ä—ā, –∑–į—Č–ĺ—ā–ĺ –ĺ–Ī—Ä—ä—Ā–Ĺ–į—ā–ł—ā–Ķ –ľ—ä–∂–Ķ –Ņ–ĺ –Ņ—Ä–į–≤–ł–Ľ–ĺ –Ĺ–Ķ –Ņ–ĺ—Ā–Ķ—Č–į–≤–į—ā –Ī—Ä—ä—Ā–Ĺ–į—Ä—Ź.
–ü–į—Ä–į–ī–ĺ–ļ—Ā—ä—ā –Ĺ–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–į—ā–į —Ā–ł–Ľ–į
–ě—Č–Ķ –Ĺ–į—Ä–ł—á–į–Ĺ –Ņ–į—Ä–į–ī–ĺ–ļ—Ā –Ĺ–į –Ĺ–Ķ—É—Ā—ā–ĺ–ł–ľ–į—ā–į —Ā–ł–Ľ–į, —ā–ĺ–Ļ —Ā–Ķ —Ą–ĺ—Ä–ľ—É–Ľ–ł—Ä–į —ā–į–ļ–į „–ö–į–ļ–≤–ĺ —Ā–Ķ —Ā–Ľ—É—á–≤–į, –į–ļ–ĺ –Ĺ–Ķ—É—Ā—ā–ĺ–ł–ľ–į—ā–į —Ā–ł–Ľ–į —Ā—Ä–Ķ—Č–Ĺ–Ķ –Ĺ–Ķ–Ņ–ĺ–ļ–Ľ–į—ā–ł–ľ–ł—Ź—ā –ĺ–Ī–Ķ–ļ—ā?“. –Ę–ĺ–Ķ—Ā—ā –Ĺ–Ķ—Č–ĺ —Ā –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–į –ľ–ĺ—Č —Ā—Ä–Ķ—Č–Ĺ–Ķ –Ĺ–Ķ—Č–ĺ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ —ā–Ķ–∂–ļ–ĺ?
–Ę–ĺ–∑–ł –Ņ–į—Ä–į–ī–ĺ–ļ—Ā —ā—Ä—Ź–Ī–≤–į –ī–į –Ī—ä–ī–Ķ —Ä–į–∑–≥–Ľ–Ķ–∂–ī–į–Ĺ —Ā–į–ľ–ĺ –ļ–į—ā–ĺ —ā—Ä–Ķ–Ĺ–ł—Ä–ĺ–≤–ļ–į –Ĺ–į –Ľ–ĺ–≥–ł–ļ–į—ā–į, –į –Ĺ–Ķ –ļ–į—ā–ĺ –Ņ–ĺ—Ā—ā—É–Ľ–į—ā –ĺ—ā –≤—ä–∑–ľ–ĺ–∂–Ĺ–į—ā–į —Ä–Ķ–į–Ľ–Ĺ–ĺ—Ā—ā. –°–Ņ–ĺ—Ä–Ķ–ī –ľ–ĺ–ī–Ķ—Ä–Ĺ–ł—ā–Ķ –Ĺ–į—É—á–Ĺ–ł –≤—ä–∑–≥–Ľ–Ķ–ī–ł –Ĺ–ł–ļ–ĺ—Ź —Ā–ł–Ľ–į –Ĺ–Ķ –Ķ –Ĺ–į–Ņ—ä–Ľ–Ĺ–ĺ –Ĺ–Ķ—É—Ā—ā–ĺ–ł–ľ–į –ł –Ĺ—Ź–ľ–į —ā–į–ļ–ĺ–≤–į –Ĺ–Ķ—Č–ĺ –ļ–į—ā–ĺ –ĺ–Ī–Ķ–ļ—ā, –ļ–ĺ–Ļ—ā–ĺ –Ĺ–Ķ –ľ–ĺ–∂–Ķ –ī–į –Ī—ä–ī–Ķ –Ņ–ĺ–ľ—Ä—ä–ī–Ĺ–į—ā. –Ē–ĺ—Ä–ł –Ĺ–į–Ļ-–Ĺ–ł—Č–ĺ–∂–Ĺ–į—ā–į –Ņ—Ä–ł–Ľ–ĺ–∂–Ķ–Ĺ–į —Ā–ł–Ľ–į –Ī–ł –Ņ—Ä–Ķ–ī–ł–∑–≤–ł–ļ–į–Ľ–į –Ĺ—Ź–ļ–į–ļ–≤–ĺ —É—Ā–ļ–ĺ—Ä–Ķ–Ĺ–ł–Ķ, –Ņ—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į–Ĺ–Ķ –Ĺ–į –ĺ–Ī–Ķ–ļ—ā —Ā –ļ–į–ļ–≤–į—ā–ĺ –ł –ī–į –Ķ –ľ–į—Ā–į, –ľ–į–ļ–į—Ä –ł —Ä–Ķ–∑—É–Ľ—ā–į—ā—ä—ā –ī–į –Ķ —ā–ĺ–Ľ–ļ–ĺ–≤–į –Ĺ–ł—Č–ĺ–∂–Ķ–Ĺ –ł —ā—Ä—É–ī–Ĺ–ĺ –ł–∑–ľ–Ķ—Ä–ł–ľ, —á–Ķ –ī–į –ļ–Ľ–ĺ–Ĺ–ł –ļ—ä–ľ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ—Ā—ā –ł–Ľ–ł –ī–į –Ķ –Ĺ–Ķ–≤–ł–ī–ł–ľ –∑–į –Ĺ–į—Ā.

–ē–ī–ł–Ĺ –Ĺ–Ķ–Ņ–ĺ–ļ–Ľ–į—ā–ł–ľ, –Ĺ–Ķ–Ņ—Ä–Ķ–ľ–Ķ—Ā—ā–≤–į–Ķ–ľ –Ņ–ĺ –Ĺ–ł–ļ–į–ļ—ä–≤ –Ĺ–į—á–ł–Ĺ –ł —Ā –Ĺ–ł–ļ–į–ļ–≤–į —Ā–ł–Ľ–į –ĺ–Ī–Ķ–ļ—ā —ā—Ä—Ź–Ī–≤–į –ī–į –Ņ—Ä–ł—ā–Ķ–∂–į–≤–į –ł–Ĺ–Ķ—Ä—Ü–ł—Ź —Ā –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ –≥–ĺ–Ľ—Ź–ľ–ĺ —á–ł—Ā–Ľ–ĺ –ł —Ā–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ–Ĺ–ĺ –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ –≥–ĺ–Ľ—Ź–ľ–į –ľ–į—Ā–į. –Ę–į–ļ—ä–≤ –ĺ–Ī–Ķ–ļ—ā –Ī–ł –ļ–ĺ–Ľ–į–Ņ—Ā–ł—Ä–į–Ľ (—Ā–Ņ–ĺ—Ä–Ķ–ī —Ā—ä–≤—Ä–Ķ–ľ–Ķ–Ĺ–Ĺ–ł—ā–Ķ —Ā—Ö–≤–į—Č–į–Ĺ–ł—Ź –∑–į —á–Ķ—Ä–Ĺ–ł –ī—É–Ņ–ļ–ł) –Ņ–ĺ–ī —Ā–≤–ĺ—Ź—ā–į —Ā–ĺ–Ī—Ā—ā–≤–Ķ–Ĺ–į –≥—Ä–į–≤–ł—ā–į—Ü–ł—Ź –ł –Ī–ł —Ā—ä–∑–ī–į–Ľ —Ā–ł–Ĺ–≥—É–Ľ–į—Ä–Ĺ–ĺ—Ā—ā. –Ě–Ķ—É—Ā—ā–ĺ–ł–ľ–į—ā–į —Ā–ł–Ľ–į –Ņ—ä–ļ –ĺ—ā —Ā–≤–ĺ—Ź —Ā—ā—Ä–į–Ĺ–į —Č–Ķ –ł–∑–ł—Ā–ļ–≤–į –Ī–Ķ–∑–ļ—Ä–į–Ļ–Ĺ–ĺ –≥–ĺ–Ľ—Ź–ľ–į –Ķ–Ĺ–Ķ—Ä–≥–ł—Ź, –ļ–ĺ—Ź—ā–ĺ –Ĺ—Ź–ľ–į –ļ–į–ļ –ī–į —Ā—ä—Č–Ķ—Ā—ā–≤—É–≤–į –≤ –Ķ–ī–Ĺ–į –ļ—Ä–į–Ļ–Ĺ–į –í—Ā–Ķ–Ľ–Ķ–Ĺ–į.


























